Patriot Viper III Review: 2x4 GB at DDR3-2400 C10-12-12 1.65 V

CPU Compute

One side I like to exploit on CPUs is the ability to compute and whether a variety of mathematical loads can stress the system in a way that real-world usage might not.  For these benchmarks we are ones developed for testing MP servers and workstation systems back in early 2013, such as grid solvers and Brownian motion code.  Please head over to the first of such reviews where the mathematics and small snippets of code are available.

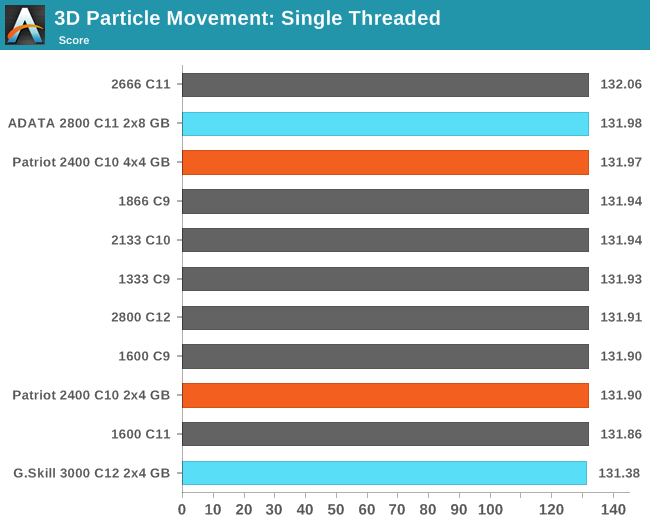
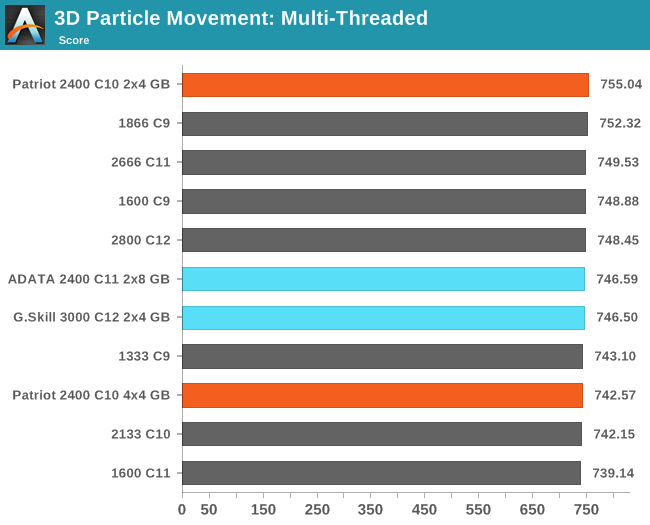
3D Movement Algorithm Test

The algorithms in 3DPM employ uniform random number generation or normal distribution random number generation, and vary in various amounts of trigonometric operations, conditional statements, generation and rejection, fused operations, etc.  The benchmark runs through six algorithms for a specified number of particles and steps, and calculates the speed of each algorithm, then sums them all for a final score.  This is an example of a real world situation that a computational scientist may find themselves in, rather than a pure synthetic benchmark.  The benchmark is also parallel between particles simulated, and we test the single thread performance as well as the multi-threaded performance.  Results are expressed in millions of particles moved per second, and a higher number is better.

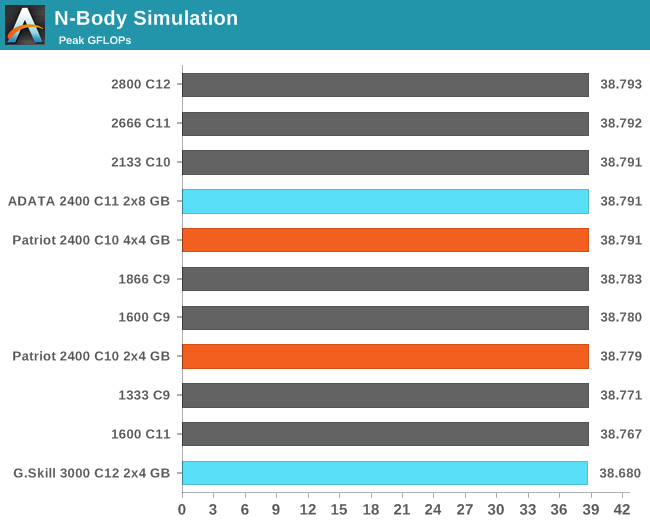
N-Body Simulation

When a series of heavy mass elements are in space, they interact with each other through the force of gravity.  Thus when a star cluster forms, the interaction of every large mass with every other large mass defines the speed at which these elements approach each other.  When dealing with millions and billions of stars on such a large scale, the movement of each of these stars can be simulated through the physical theorems that describe the interactions.  The benchmark detects whether the processor is SSE2 or SSE4 capable, and implements the relative code.  We run a simulation of 10240 particles of equal mass - the output for this code is in terms of GFLOPs, and the result recorded was the peak GFLOPs value.

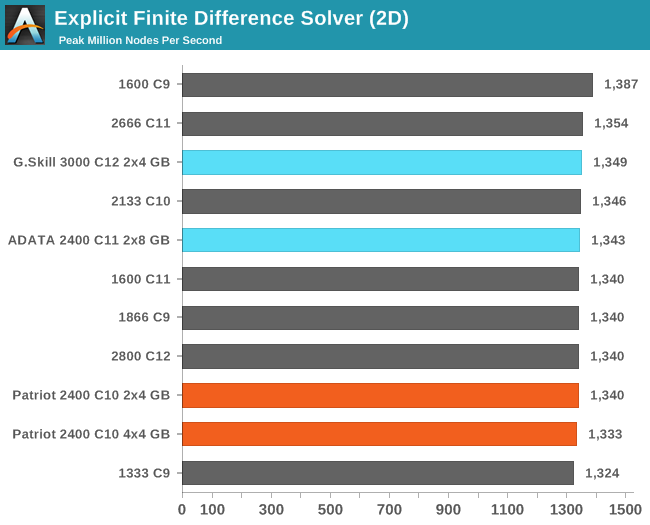
Grid Solvers - Explicit Finite Difference

For any grid of regular nodes, the simplest way to calculate the next time step is to use the values of those around it.  This makes for easy mathematics and parallel simulation, as each node calculated is only dependent on the previous time step, not the nodes around it on the current calculated time step.  By choosing a regular grid, we reduce the levels of memory access required for irregular grids.  We test both 2D and 3D explicit finite difference simulations with 2ⁿ nodes in each dimension, using OpenMP as the threading operator in single precision.  The grid is isotropic and the boundary conditions are sinks.  We iterate through a series of grid sizes, and results are shown in terms of ‘million nodes per second’ where the peak value is given in the results – higher is better.

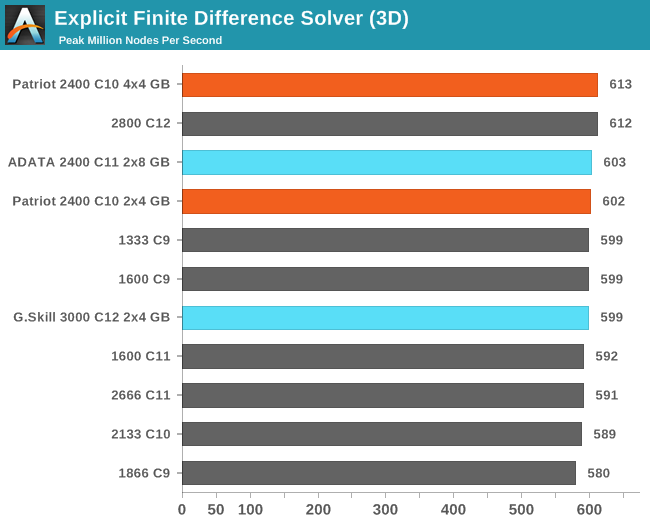
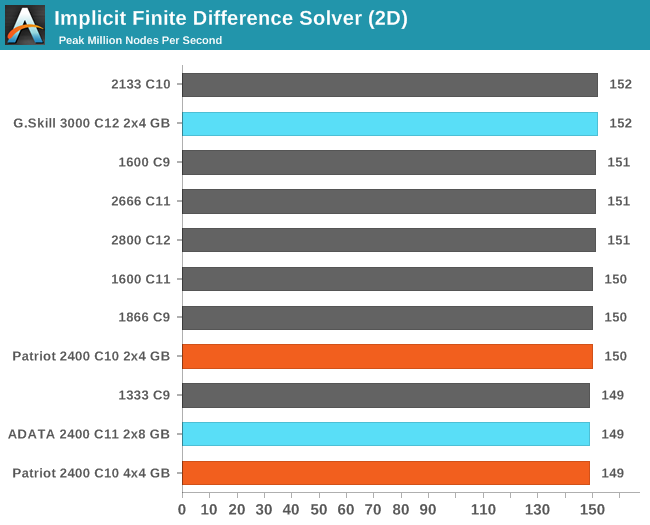
Grid Solvers - Implicit Finite Difference + Alternating Direction Implicit Method

The implicit method takes a different approach to the explicit method – instead of considering one unknown in the new time step to be calculated from known elements in the previous time step, we consider that an old point can influence several new points by way of simultaneous equations.  This adds to the complexity of the simulation – the grid of nodes is solved as a series of rows and columns rather than points, reducing the parallel nature of the simulation by a dimension and drastically increasing the memory requirements of each thread.  The upside, as noted above, is the less stringent stability rules related to time steps and grid spacing.  For this we simulate a 2D grid of 2ⁿ nodes in each dimension, using OpenMP in single precision.  Again our grid is isotropic with the boundaries acting as sinks.  We iterate through a series of grid sizes, and results are shown in terms of ‘million nodes per second’ where the peak value is given in the results – higher is better.